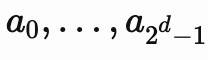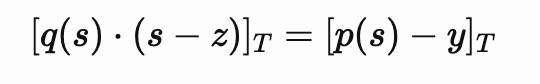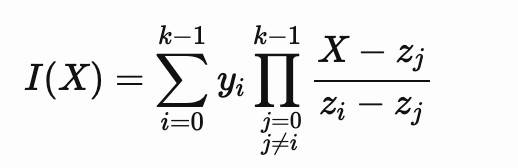技术解读实现无状态版以太坊的「Kate 多项式承诺」

本文从技术视角介绍一种「Kate多项式承诺」的密码学方案，此方案正用于研究实现无状态以太坊。

原文标题：《【他山之石】Kate多项式承诺（polynomialcommitments）》
编译：币安中国区块链研究院

本文已取得作者授权，并由链闻和币安中国区块链研究院获得中文地区翻译首发权

在本文拟介绍Kate、Zaverucha和Goldberg所提出的承诺方案（commitmentscheme）1。但作为一篇介绍性文章，本文无意做严谨、完整的数学或密码学论述。

该方案通常被称作「Kate多项式承诺方案」，是多项式承诺方案的一种。它支持验证人计算对多项式的承诺，可通过其属性在任意后续位置开启此承诺：验证人需要证明多项式在某位置上的值均等于声明值。

验证人一旦将承诺值（椭圆曲线点）发给了校验人，便无法再更改相应的多项式，因此得名「承诺」。校验人只能提供多项式的有效证明；若尝试作弊，要么无法得出证明，要么证明会被校验人拒绝。

预备知识

强烈推荐不熟悉有限域、椭圆曲线与配对的读者提前阅读VitalikButerin有关椭圆曲线配对的文章。

与默克尔树（Merkletree）的对比

若读者熟悉默克尔树，本人希望可以更直观地呈现默克尔树与Kate承诺之间的差别。用密码学家的话来说，默克尔树是一种向量承诺（vectorcommitment）：你可以使用一个深度为d的默克尔树，计算出对向量

（即一系列固定长度的元素）的承诺。你也可以运用默克尔证明，借助d散列，证明位于i处的元素ai是该向量的一部分。

实际上，我们可以通过默克尔树得出多项式承诺：次数为n的多项式p(X)只是一个函数

其中pi是多项式的系数。

通过设置ai=pi并计算其系数的默克尔根，可以很容易地得出次数为n=2d-1时的多项式。证明求值指的是验证人想要告诉校验人：对于某个z，p(z)=y。对此，验证人可以把所有的pi值都发给校验人，然后校验人计算得出p(z)确实等于y。

当然，这是一个非常低级的多项式承诺，但能帮助我们理解其具有哪些优势。观察下面这些属性：

1.承诺大小是一个单散列（默克尔根）。一个足够安全的加密散列通常需要256个位元（bit），即32个字节（byte）。
2.要想证明一个求值，验证人需要把所有的pi发出去，以此证明大小（proofsize）与多项式的次数呈线性关系，校验人需要进行线性运算（通过计算

求出多项式在位置z处的值）。

3.此方案未对多项式进行隐藏——验证人以非隐藏方式发送完整的多项式，及其每一个系数。

下面，我们探讨一下Kate方案以此类指标可以实现怎样的效果。

另外，也可以把任意求值的证明合并到一个群元素中。正是这些属性使Kate方案通行于PLONK、SONIC等零知识证明系统，也使之可以作为向量承诺适用于一般情况。下文将予以详述。

椭圆曲线与配对

如上所述，本人强烈推荐VitalikButerin有关椭圆曲线配对的文章，其中介绍了理解本文所需的所有预备知识，尤其是有限域、椭圆曲线与配对等方面。

假设G1和G2为带有配对e的两条椭圆曲线：G1×G2→GT。G1和G2的阶数均为p，生成元（generator）分别为G和H。用简化符号分别记作

[x]1=xG∈G1和[x]2=xH∈G2

任意x∈Fp。

可信设置（Trustedsetup）

假设完成了可信设置，则在某个秘密点s上，验证人和校验人均能获得i=0、……n-1时的[si]1和[si]2元素。

你可以这样理解这种秘密设置：用一台气隙计算机（airgappedcomputer）计算随机数s，计算所有的群元素[si]x，然后用有线方式只把这些元素发出去（不发送s），最后把这台计算机销毁。当然，这种方案不够完美，因为你必须信任计算机操作员不会通过秘密通信通道获取到秘密点s的值。

在实践中，这通常是通过安全的多方计算（MPC）来实现的，此方法允许由一组计算机创建此类群元素，从而杜绝任何计算机获取秘密点s的值，而要想获取到s，需要所有的计算机联手（或同时被攻破）才能做到。

注意，不会出现以下情况：即仅通过选择某个随机群元素[s]1（其s未知），计算出其他的群元素，最后得出s。在s未知的情况下，无法计算出[s2]1。

现在，椭圆曲线加密基本上说明了不可能通过可信设置的群元素得出s的实际值。s是Fp中的一个数，但是验证人不可能找出这个数的实际值。验证人只能根据提供给他们的元素执行特定的计算。因此，验证人可以通过椭圆曲线乘法运算，很容易地计算出c[si]1=csiG=[csi]1等，且由于可以加上椭圆曲线点，还可以计算出c[si]1+d[sj]1=(csi+dsj)G=[csi+dsj]1等。实际上，如果

是多项式，验证人可以计算出：

有趣的是，几乎每个人都能使用这种可信设置在s未知的情况下，求出多项式在秘密点s处的值。除非他们没有得到自然数输出，而是只得到椭圆曲线点[p(s)]1=p(s)G，但是这就已经非常强大了。

Kate承诺

在Kate承诺方案中，元素C=[p(s)]1是对多项式p(X)的承诺。

或许你会问：（在s未知的情况下）验证人能否找到另一个具有相同承诺的多项式q(X)≠p(X)，即[p(s)]1=[q(s)]1？假设存在这种情况。那将意味着[p(s)-q(s)]1=[0]1，说明p(s)-q(s)=0。

现在，r(X)=p(X)-q(X)本身就是一个多项式。我们知道因为p(X)≠q(X)，所以其并非常数。众所周知，任何次数为n的非常数多项式最多可以有n个零：因为如果r(z)=0，则r(X)可被线性因子X-z整除；因为我们可以将每个零除以一个线性因子，并且每除一次会使次数减一，所以次数不会超过n。^2

由于验证人不知道s，因此实现p(s)-q(s)=0的唯一方法是在尽可能多的位置上实现p(X)-q(X)=0。但是，正如以上证明，由于验证人最多可以选n个位置，所以成功的可能性不高：由于n值远小于曲线p的次数，因此他们不太可能选择s点来使p(X)=q(X)。为了感受此概率，假设采用当前可实现的最大可信设置，其中n=228，并将其与曲线阶数p≈2^256进行比较：即便攻击者通过精心设计，使多项式q(X)在最多n=228个点上等于p(X)，使这个多项式得出相同承诺（p(s)=q(s)）的概率也只有228/2256=2^28-2^56≈2·10-69。概率极低。这其实就意味着攻击者无法实现其意图。

多项式相乘

到现在，我们已经证明了能够求出多项式在秘密点s处的值，这使得我们能够对一个唯一的多项式做出承诺——在某种意义上，尽管具有相同承诺C=[p(s)]1的多项式不止一个，但在实际中是无法计算出来的（密码学家称之为计算绑定（computationallybinding））。

不过，在不将多项式完整地发送给校验人的情况下，我们仍无法「开启」承诺。而要「开启」承诺，我们需要用到配对。如上所述，我们可以用秘密元素进行某些线性运算；例如，我们可以把[p(s)]1计算为对p(X)的承诺，也可以把p(X)和q(X)的两个承诺相加，得出合并承诺p(X)+q(X)：[p(s)]1+[q(s)]1=[p(s)+q(s)]1。

现在我们无法将两个多项式相乘。否则，就能使用多项式的某些属性实现目标。尽管椭圆曲线本身做不到，但所幸，我们可以通过配对来实现：我们知道：

其中引入了新符号[x]T=e(G,H)x。因此，虽然我们不能把椭圆曲线里的两个域元素简单地相乘，然后将其乘积当作一个椭圆曲线元素（这是所谓的全同态加密（FHE）的属性之一；而椭圆形曲线仅是加法同态的），但是，如果在两个不同的曲线中对它们（一个在G1中，一个在G2中）进行承诺，并且输出是一个G元素的话，我们就能把两个域元素相乘。

这时就触及到了Kate证明的核心：还记得我们之前提到了线性因子么：如果多项式在z处为零，则多项式可被X-z整除。显然，反过来也是如此——如果多项式可被X-z整除，那么多项式在z处显然为零：被Xz整除意味着：我们可以得出某些多项式q(X)的p(X)=(X-z)-q(X)，且多项式在X=z处显然为零。

现在要证明p(z)=y。我们接着使用多项式p(X)-y——由于该多项式在z处显然为零，因此我们可以运用线性因子的相关知识。使q(X)等于多项式p(X)-y，被线性因子X-z整除，即

即等同于q(X)(X-z)=p(X)-y。

Kate证明

现在，将p(z)=y求值的Kate证明定义为π=[q(s)]1。对多项式p(X)的承诺被定义为C=[p(s)]1。

校验人使用以下公式检查此证明：

注意，校验人可以计算出[s-z]2，因为[s-z]2只是来自可信设置的元素[s]2与z的组合，且z是多项式的求值点。同样，把y当作声明值p(z)，便可以计算出[y]1。那么，为什么此检查能使校验人相信p(z)=y；更准确地说，是使校验人相信由C所承诺的多项式在z处求出的值为y？

我们需要评估两个属性：正确性和可靠性。正确性指验证人执行我们定义的步骤，可以得出能通过核验的证明。这一点一般不难。可靠性指校验人无法得出「不正确」的证明，即无法使校验人相信当y'≠y时，p(z)=y′。

首先，写出配对群中的方程式：

其正确性现在应该很明显了，即在未知随机点s上需要求值的方程q(X)(X-z)=p(X)-y。

那么，我们怎么证明其可靠性以及验证人无法创建假证明呢？我们要用多项式思路来思考这个问题。如果验证人按我们的方法来构造证明，就必须以某种方式使p(X)-y′被X-z整除。但是p(z)-y′不为零，因此无法进行多项式除法运算，因为总会有余数。所以，这种方法显然行不通。

至此，就要尝试椭圆群：如果能计算出某些承诺C的椭圆群元素，结果又会怎样？

很显然，如果做到了这一点，就能证明一切。凭直觉来看，这一点很难实现，因为必须将与s相关的某些值指数化，但是s是未知的。出于证明的周密性考虑，需要提出配对的密码学假设，即所谓的q-SDH假设3。

多值证明（Multiproofs）

现在，我们已经演示了如何证明多项式在一个点上的求值。注意，这已经非常了不起了：通过仅发送一个单群元素（例如，BLS12_381中有48个字节），就能证明某个具有任意个次数（假设228个）的多项式在某个点上包含了某个值。在将默克尔树当作多项式承诺的小例子中，需要发送228个元素——多项式的所有系数。

现在，我们要更进一步，证明可以在任意数量的点上求出多项式的值，且仍然只使用一个群元素即可。为此，我们需要引入另一个概念：插值多项式。假设有一系列的k值(z0,y0)、(z1,y1)……(zk-1,yk-1)：然后，总是能找到一个次数小于k的多项式能通过所有这些点。实现方法之一是使用拉格朗日插值法，此方法为该多项式I(X)提供了一个明确的公式：

现在，假设已知p(X)通过了所有点。则多项式p(X)-I(X)在z0、z1……、zk-1处均明显为零。这意味着它可以被所有线性因子（X-z0）、（X-z1）……（X-zk-1）整除。我们把所有因子都合并到所谓的零多项式中

就可以计算商数了

注意，这是可行的，因为p(X)-I(X)可被Z(X)中的所有线性因子整除，因此它可被整个Z(X)整除。

我们现在可以给求值(z0,y0)、(z1,y1)……(zk-1,yk-1)：π=[q(s)]1定义Kate多值证明——注意，这里仍然只有一个群元素。

现在，要进行检查，校验人还必须计算插值多项式I(X)和零多项式Z(X)。借此，他们可以计算[Z(s)]2和[I(s)]1，从而校验配对方程式

通过写出配对群中的方程，可以轻松地校验其能否以与单点Kate证明相同的方式进行验证：

其效果惊人：只需提供一个群元素，就可以证明任何数量的求值达一百万次！仅48字节即可证明所有求值！

用作向量承诺的Kate承诺

虽然Kate承诺方案被设计成了一种多项式承诺，但实际上也能成为非常好的向量承诺。向量承诺对向量a0……an-1进行承诺，为证明自己对某个i承诺了ai提供了方法。可以使用Kate承诺方案来进行重现：使p(X)为所有i均取为p(i)=ai的多项式。我们现在得到了这样一个多项式，可以用拉格朗日插值法来计算它：

利用这个多项式，我们可以仅使用一个群元素就能证明向量中任意数量的元素！（仅就证明大小而言）这种方法的效率要比默克尔树高得多：仅证明一个元素，一次默克尔证明会消耗logn个散列！

延伸阅读

我们目前正在研究如何利用Kate承诺打造出无状态版的以太坊。因此，本人强烈建议在ethresearch论坛中搜索Kate，查找与当前研究相关的话题。

除本文外，Vitalik对PLONK的介绍也非常精彩，其中大量使用了多项式承诺，并采用了Kate方案作为主要示例。

1.https://www.iacr.org/archive/asiacrypt2010/6477178/6477178.pdf

2.此结果常被错误地引用做代数基本定理。而代数基本定理刚好相反（仅在代数闭域中有效），在复杂的数值中，每一个次数为n的多项式都有n个线性因子。但是，尽管此处简化结果对于代数学有重要意义，但还缺少一个简洁、朗朗上口的名称。

3.https://www.cs.cmu.edu/~goyal/ibe.pdf

来源链接：dankradfeist.de

本文来源：币安研究院
原文标题：技术解读实现无状态版以太坊的「Kate 多项式承诺」

—-

编译者/作者：币安研究院

玩币族申明：玩币族作为开放的资讯翻译/分享平台，所提供的所有资讯仅代表作者个人观点，与玩币族平台立场无关，且不构成任何投资理财建议。文章版权归原作者所有。